
With this information I can identify the initial amount of radium as 50 grams and the time to be 630 years. Given information: If 50 grams are present now, how much will be present in 630 years? Part 2: Answer the question using the rest of the given information. Note: Although I have put an approximation for k here, try not to round until the very last step. Using only the information about radium having a half-life of 1690 years I have found the decay rate for radium. Solve for the decay rate k: Solve for k by dividing by 1690 on both sides Solve for the decay rate k: Simplify ln e = 1 Solve for the decay rate k: Use the power rule for logarithms to get k out of the exponent Solve for the decay rate k: Take the natural log of both sides to get k out of the exponent Solve for the decay rate k: Start by dividing both sides by the coefficient to isolate the exponential factor Make a substitution for A and t since it is known that the half-life is 1690 years and Substitute these values into the exponential decay formula and solve for k.

The amount after 1690 year is half of the initial amount.

This allows me to establish a relationship between the initial amount and the amount after 1690. Since radium has a half life of 1690 years, we know that after 1690 years there will be half of the initial amount of radium left. Since we are using an exponential model for this problem we should be clear on the parts of the exponential decay model.

Part 1: Use some of the information to find the decay rate of radium.
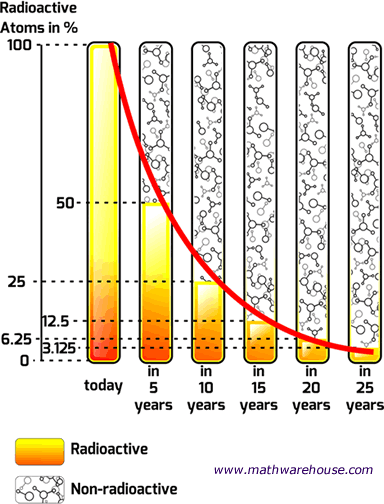
Solution: There is a two part process to this problem. If 50 grams are present now, how much will be present in 630 years? Example: The half life of radium is 1690 years.


 0 kommentar(er)
0 kommentar(er)
